nameskvm.blogg.se - Matrix in r

The solve() function takes a matrix as input and returns the matrix’s inverse as output. But we can do matrix multiplication, with the %*% operator. We can perform the element-wise multiplication of two matrices using the * operator. The is.matrix() function takes an object as input and returns TRUE if the object is a matrix.

colMeans(), rowMeans(), and mean() functions.

colSums(), rowSums(), and sum() functions.

The major one that we are going to discuss today are: There are a lot of matrix functions in R. What are the Matrix Functions in R?įunctions that take a matrix as input or return a matrix as output are called matrix functions. We can create a matrix using the matrix() function. They have a dimattribute that defines their dimensions. They can store values of the same data type in the form of rows and columns. Logic Statements (TRUE/FALSE) and cbind and rbind Command in R (R Tutorial 1.In R, matrices are two-dimensional data structures.

What's the mean of the first row of matrix z?.

Create a matrix, say z, composed of x as the first column and y as the second column.

Suppose we have two vectors, x and y, defined as follows. The cbind() function is used to combine the variables such that its output contains the original variables in columns while rbind() combines the variables such that its output contains the original variables in row.įor example, the following commands will create the same matrix as x. Other commonly used approaches to create matrix are cbind() and rbind(), which are counterparts of the c() function.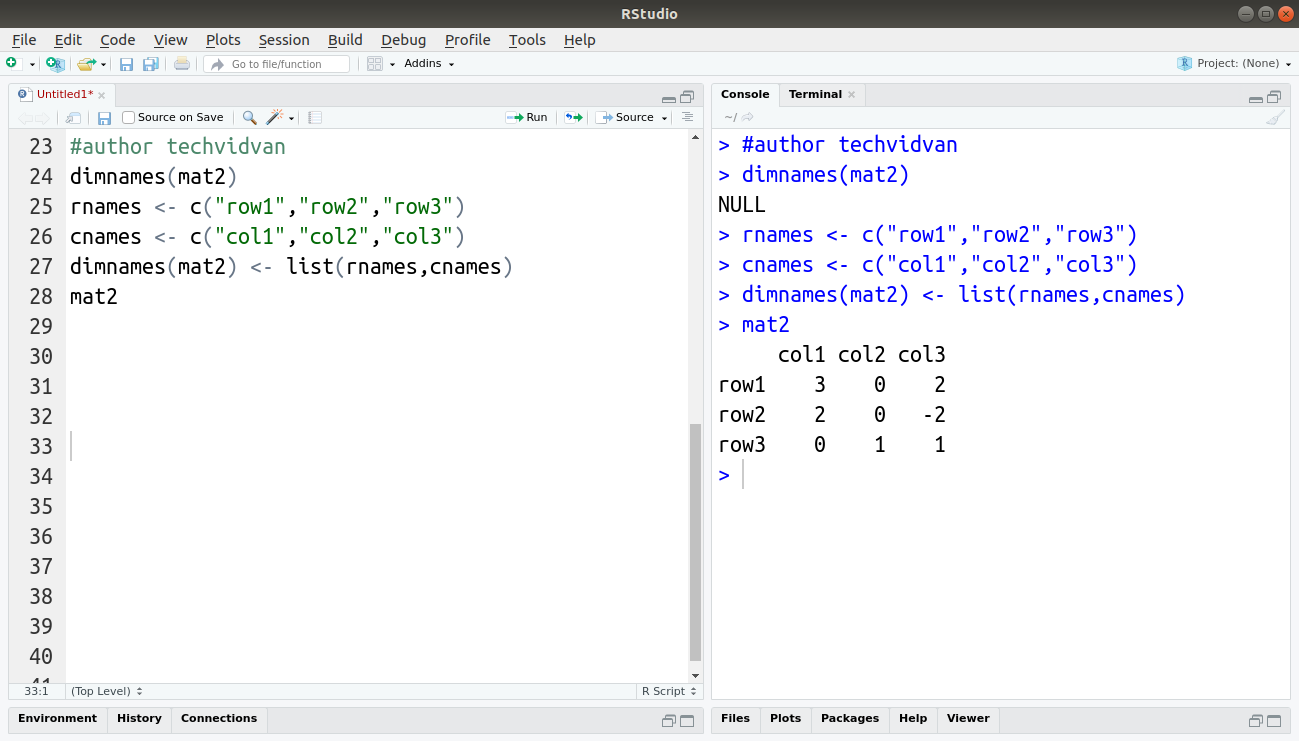

If we don't specify any element in the index, R will return all the elements. These commands can be used to call the element of 3 rd row and 2 nd column in matrix x.

We can use the commands below to extract portions of the matrix: Where the parameter ncol is the number of columns in this matrix, and the numbers are entered by default column-wise.

A two-dimensional matrix might be envisioned as a table with columns and rows, and a three-dimensional matrix might be envisioned as a series of tables stacked on top of one another.Ī matrix can be created in a number of ways. Matrices are a multi-dimensional vectors. The vectors that have been discussed previously in this module were one-dimensional, i.e., they consisted of a simple series of elements that you could imagine being organized in a single row or in a single column.